Large uncertainties due to insufficient covid-19 test in NYS
In mid Jan 2020, the first case of covid-19 was confirmed in US (in WA). The first handful of cases confirmed following this were mostly concentrated in Washington state and California. It was “puzzling” that NY state did not have any cases, given the population density and the number of travelers, while the number of cases in WA and CA continued to increase. The first case in NYS was confirmed on March 1st 2020. Even after this first case, WA and CA continued to have the most cases across US. It took ~2+ weeks for NYS to be the leading state. Why is that? This seems contradictory to our intuition that NYC is the most densely populated city in the entire US and there are a few international airports within 100 miles. This puzzle can understood by acknowledging that the government is totally unprepared for covid-19.
There were limited number of covid-19 test kits available across US. Even in mid March, there were only 5 tests available per million people in US. As of last Saturday (March 14, 2020), only ~21,000 tests were carried out across US! On the other hand, there were ~3700 tests available per million people in South Korea, where ~20,000 people are being tested per day! Among the ~21,000 tests done across US by last Saturday, only ~3,300 of them are from NYS. Note that this is 10 days after the first confirmed case in NYC and NYS. The fact that only 3,300 tests were conducted across the New York state since then is concerning. As soon as more covid-19 tests were available, the number of confirmed cases in NYS skyrocketed. It is now the leading state across US! Gotham City is now the epicenter of covid-19 in US!
The lack of covid-19 tests has led to a severily underestimation in the number of covid-19 infections in US. Based on the data from China, South Korea, and European countries, where the covid-19 outbreak started around Jan 2020, it’s estimated that the incubation period is ~14 days and that on average, a sick person will transmit the virus to ~2-4 other people. Taking these numbers and fitting a model to the time series of confirmed cases in US, we can estimate how many people might have covid-19 (but remains unknown due to the lack of covid-19 test kits).
In the following, I will perform such estimation for New York State.
Modeling the growth rate in NYS as exponential
After scraping some data on the number of confirmed cases of covid-19 in US, I separate out the NYS from the other states and fitted an exponential function to the time series.

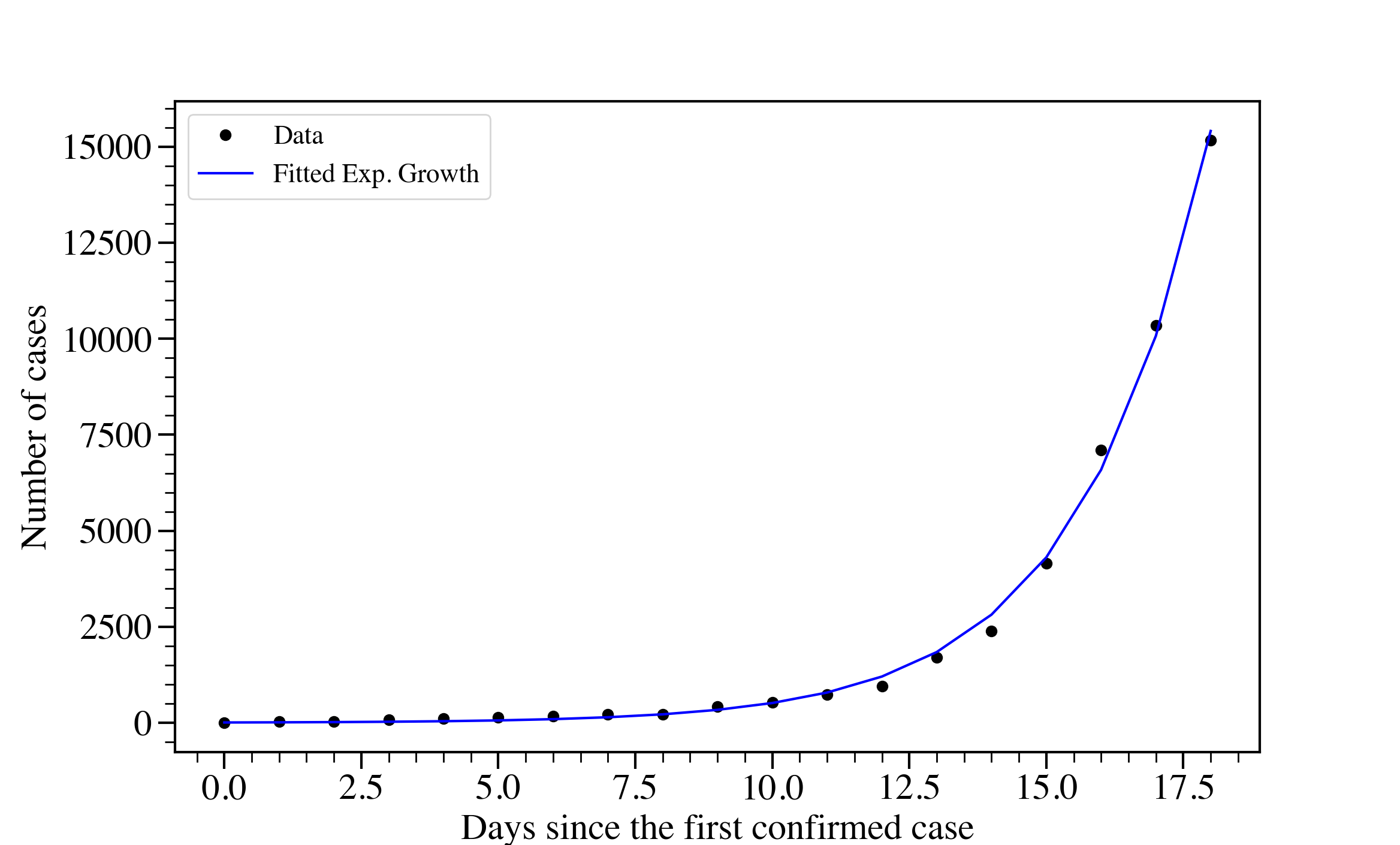
In fact, the trend follows an exponential growth! This is alarming!
Inverting the exponential function to estimate the number of unknown infections
We can then invert the function to calculate, given the cumulative number of known cases to date, what’s the actual total number of cases (including unknown ones) that already exist.
We introduce two variables, one is “days_infected_before_outcome” and another is “total_cases_days_before_outcome”. These two variables are introduced because up to date, we have no idea what’s the percentage of population that could be infected with covid-19 (unless extensive testing is being done and tracks how it’s transmitted among the population), the closet number we know for a fact is the number of deaths to-date. If we adopt a death rate, which I assume to be 0.7% following the seasonal flu (since we don’t know the number fo covid-19), we can equate this “assumed_death_rate” to “number_of_death_to_date”/”number_total_infected”. But note that “number_total_infected” is the “total_cases_days_before_outcome”, there’s a lag in time between the outcome (death) and the infection rate (current). Thus, when we want to determine the number of infections (current) from the death rate, we would have to account for this time lag (“days_infected_before_outcome”). Using data from other countries on covid-19, we assume “days_infected_before_outcome” = 14 days.
Using the coefficients from the best-fitted exponential function, we can use an inverse exponential function to determine, given the cumulative “total_cases_days_before_outcome”, how many days has it been since the first detected case by the time we have “total_cases_days_before_outcome”. We then account for the time lag to find out the current number of total cases (be it unknown or known).

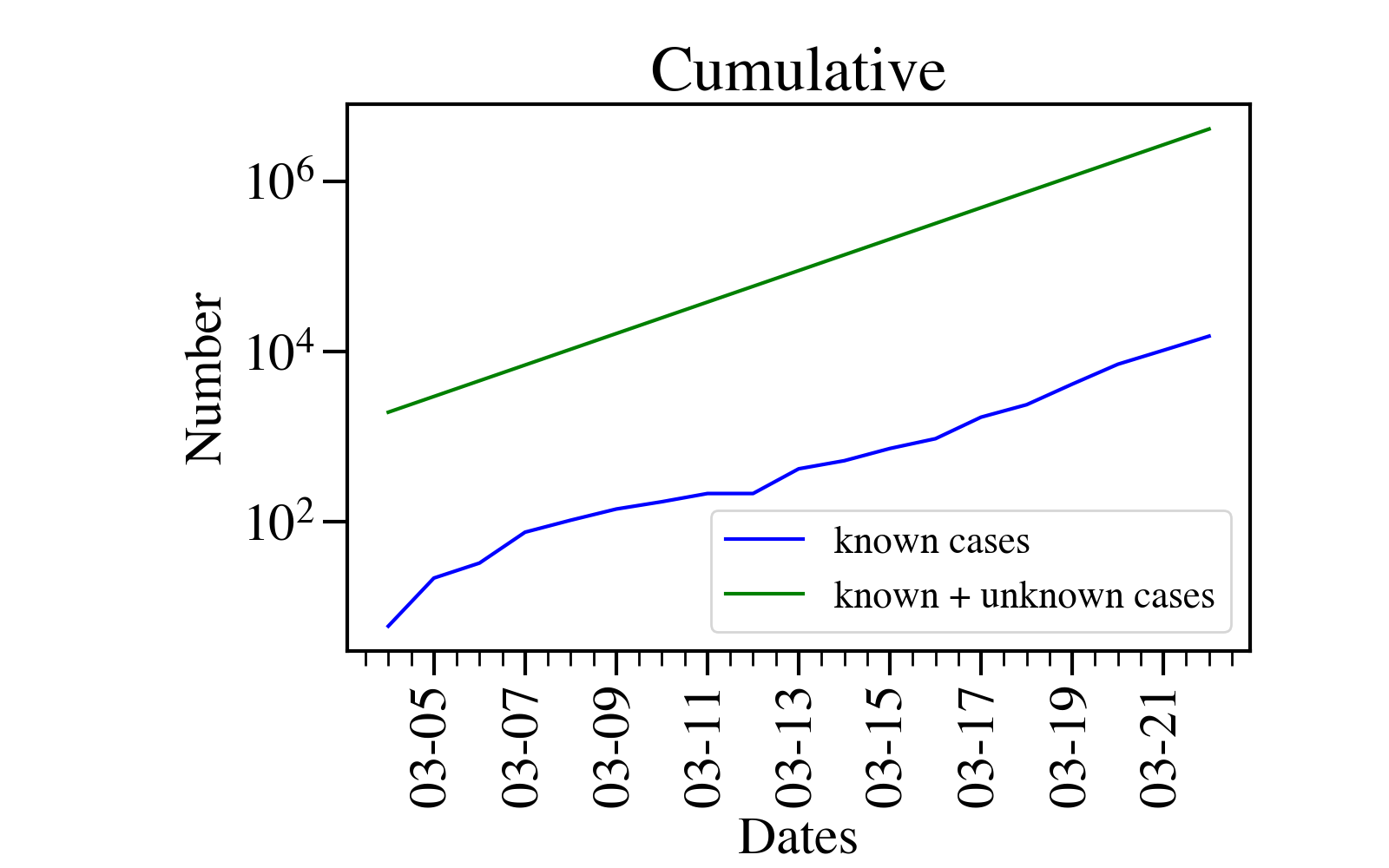
Based on this model and these assumptions, namely, the death rate follows seasonal flu and that the delay between an infection and death is 14 days, we find this differences between known cases (blue line) and the actual number of cases (green line) in NYS. Clearly, there’s a huge number of unknown cases out there! Despite the uncertainties in the two assumptions I have made, within an order of magnitude, the number of known cases in NYS is at least 30 time less than the actual number!